|
SME Light Winter Quarter Lecture 7: What is Polarized Light? Tuesday, January 25th, 2000 Outline (to put on the board during lecture)
I. 3-D glasses and how they work Materials that would be cool for demos during this lecture:
Notes to Lecturer:
A. 3-D vision Why is it that we see 3-D in everyday life, without 3-D glasses? Remember from fall that we have 3-D vision because our eyes get two different perspectives on the world, and our brain uses the difference between these views to figure out how far away from us something is. If something is very far away, our two eyes will get approximately the same perspective on it. But if it is close, then it will look very different to our two different eyes. For a dramatic example of this, close one eye, hold up your thumb, and align it so that it is exactly covering one of the lights in the room. Now close the eye you were looking with and open the other eye. The reason that the light is no longer aligned with your thumb is that your other eye has a different view of the world than the first eye. The two and a half inches between your eyes may not seem like much, but it makes a big difference!! (Remember the dental floss in lab #1 from fall.) In the background, your brain is ascertaining how far away from you an object is by how different it looks to your two eyes. Have you ever noticed that if you cover up one eye you lose perspective on distances? Try it sometime. A good trick is to try to touch two pencils end to end (eraser ends are easier than point ends of course) with both eyes open and then with one eye open. It's a lot harder with just one eye! B. Stereoviewers So to see a picture in 3-D, you need your two eyes to see two different images, and those images need to be offset from each other by the amount that they would be offset in real life. But how can you get your two eyes to see two different images? The way people used to do it was using a "stereoviewer" like this one. A stereoviewer is a device that separates the views seen by your two different eyes. C. 3-D glasses years ago (blue and red filters) Another way to see a picture in 3-D would be to use red and blue filters. Can you think of how red and blue filters could be used to make you see in 3 dimensions? D. 3-D glasses today (plane polarized light) 1. What is plane polarized light? We've talked about light as an oscillating electric field going up and down in a wave:
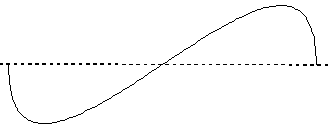 We drew the wave in the plane of the page because it was convenient. But light waves aren't always traveling in the same plane. Waves can travel in any plane they want. BREAK-OUT SESSION: These "polarizing filters" only let through the light that is traveling straight up and down perpendicular to the plane of the filter. What will happen if I align the two filters perpendicular to each other? Align the filters perpendicular and observe that they block the light. Show also that they transmit maximally when they are aligned parallel to each other. One good way to think about how waves can be in any plane is to draw them on pieces of board. You can orient the board any way you want, but if you try to shove it through a picket fence, only the board that's oriented correctly will get through (see the picture below).
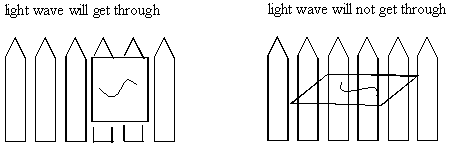 THIS MODEL ILLUSTRATES THE PHENOMENON WELL BUT HAS SOME LIMITATIONS!! Taken literally, this picture might make you think that if you have two filters, light will get through both only if the filters are in exactly the same orientation. Two fences at a slight angle should stop all boards. The reason this is misleading is that if the light wave is not exactly vertical and not exactly horizontal, then some of the light will still get through the polarizing filter. We would say that the part or component of the light that is vertical would make it through the filter. You can see why this wouldn't work for boards and picket fences.
 2. How is plane polarized light used to create 3-D images? Say you have two slides, one taken from each perspective, and light from one is plane polarized in one direction and light from the other one is plane polarized in the perpendicular direction. You shine these two slides at a screen, and when the light reflects off the screen it keeps its polarization. (In order to have plane polarized light keep its polarization when bouncing off the screen, the screen needs to be silver. White screens depolarize the light. Some people achieve the silver-screen effect by spray-painting white screens silver.) BREAK-OUT SESSION: Why do you see this image in 3-D when you put on the 3-D glasses? (Pass out the 3-D glasses for the students to play with as they work on this problem. It would be best to have a 3-D slide up on the screen as they work on this also.) Explain that one side of the glasses lets through one polarization of light and the other side lets the other through. If the students haven't already discovered this, point out that if one person looks through her 3-D glasses at another person with 3-D glasses, the other person's glasses will have one completely black side and another transparent side. II. The circularly polarized components of plane polarized light When we imagine light waves, it is common to have a picture of plane polarized light in our heads. But this is only one of the ways in which we can visualize light. An alternative would be to think of the light wave as a sum of circularly polarized components. In order to understand this, we'll have to understand a little bit about vector addition. BREAK OUT SESSION: If you add one arrow to another arrow pointing in the same direction, you wind up with a big arrow. If you add one arrow to another arrow pointing in the opposite direction, you wind up with nothing.
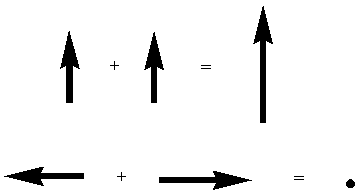 What do you think you'll wind up with if you add these two arrows?
 The horizontal components exactly cancel out, and the vertical components add together to make an arrow pointing straight up. BREAK OUT SESSION: Plot the sum of each pair of vectors above that pair of vectors. Every second pair is shaded to help you distinguish the pairs.
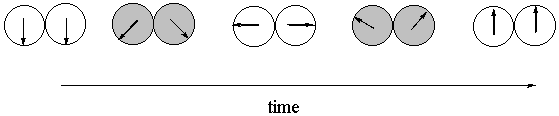 Answer:
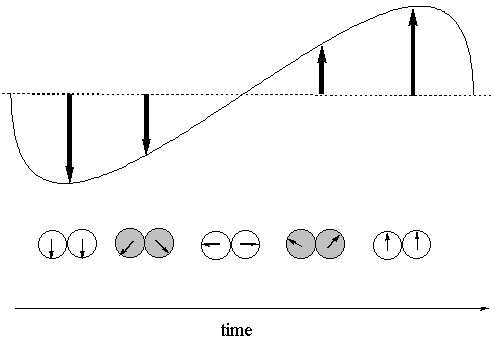 The pairs above represent what is called circularly polarized light. For example, if you look at the left-hand vector of each pair as a function of time, you will notice that it is rotating clockwise. If you look at the right-hand vector of each pair as a function of time, you will notice that it is rotating counter-clockwise. It is difficult to picture circularly polarized light because it doesn't fit neatly into the plane of the paper. In the notation above, we show the circularly polarized light by taking snapshots over time of what we would see if we looked at it head-on. Break-out session: What would circularly polarized light look like from the side? Answer: A spiral. Notice that when we add up two oppositely-circularly-polarized components of light, we get plane polarized light!! So all that stuff we told you about light as a wave whose electric field is propagating up and down like a sine wave is true, but it isn't the whole story: plane polarized light can also be conceptualized as the sum of two circularly polarized components. We will see over the course of the next few lectures why it is so important that light has circularly polarized components. Because of these spirals, light is what we call "handed," and that has vast implications for the ways in which it interacts with biological molecules.
|